证明的魔法

皮亚杰：“数学认识论有三个传统的主要问题：数学虽然是奠基于极少数内容相当贫乏的概念或公理之上，为什么却这样富有成效呢；尽管数学具有建构特性，这可能成为不合理性产生的根源，但为什么数学仍然具有必然性从而保持恒常的严格性呢；尽管数学具有完全演绎的性质，为什么数学跟经验或物理现实是符合一致的呢？”

M•克莱茵：“希腊人坚持演绎推理是数学证明唯一的方法，这是对人类文明最重要的贡献，它使数学从木匠的工具盒、测量员的背包中解放出来，使得数学成为人们头脑中的一个思想体系；从此，人们开始靠理性，而不是感官去判断事物；正是这种理性精神，开始了西方文明。”

数学能够毋庸置疑地证明事物的正确性，不仅可以肯定地证明事物，还可以证明有些事物是不可能的。

例1存在两个无理数a,b,使得a^b是有理数。

例2一种骨牌刚好可以覆盖棋盘上两个相邻的正方形格子。骨牌不允许叠加，也不允许越过棋盘边界。如果在这种情况下仍旧可以用骨牌填满棋盘，我们就将这种情况称为“平铺”。

⑴如图1，8×8棋盘请给出一种平铺的方法.

⑵如图2，8×8棋盘移除了位于一条对角线尽头的两个正方形格子，这种情况是否还能用1×2的骨牌平铺，你能证明吗？

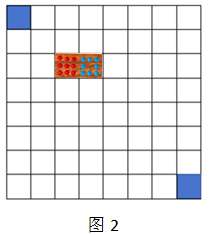
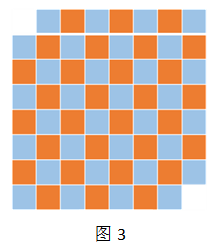
答案：如图3，因为每个骨牌覆盖相邻两个方格，将棋盘相邻两格用灰黄两种颜色交错涂色，对角线尽头的两个格子同色，所以有32个灰色，30个黄色。而每个骨牌必须同时覆盖两种颜色，于是多出来的两个灰色无法覆盖。
变式1：在7×7棋盘中，每个格子上都有一匹马。这种情况下，可以让每一匹马同时踏出符合国际象棋规则的一步吗？（规则是在纵横两个中的一个方向上踏出一格的距离，在另一个方向上踏出两格的距离）

变式2：在4×7棋盘中，你能否同时使用7个不同的俄罗斯方块（4个小格子一共可以拼接出7种图案）实现平铺？

变式3：考虑一个由512个小立方体组成的8×8×8的大立方体。假如我们移除了位于某条对角线尽头的两个小立方体，你能否用1×1×3的长方体平铺剩余部分？

例1虽然没有具体指出哪两个无理数，但毋庸置疑地证明了存在性；例2无需穷尽所有的平铺方法，但毋庸置疑地证明了不可能。这样的思维方式与数学归纳法非常相似，这是数学推理的理性与纯粹！

例3 证明：对于任意正整数n,2^n×2^n的棋盘无论在什么地方挖掉一个1×1的正方形，余下的都可以用若干个“trominos”（这是一个由 3 个方 block 组成的 L 形图形）平铺。

分析：对于2×2，无论挖掉哪一个1×1的正方形，都可以用一个“trominos”平铺，对于4×4，假设在左上角挖掉某个1×1的正方形，阴影部分用一个“trominos”平铺，所以结论成立。

一般地，可以用数学归纳法证明：

⑴当n=1时，结论成立；

⑵假设当n=k时，结论成立，对于2^{(k+1)}×2^{(k+1)}棋盘，如图，在左上角的2^k×2^k中，无论在什么地方挖掉一个1×1的正方形，余下的都可以用若干trominos”平铺。

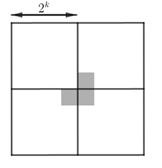
在增加的三个2^k×2^k棋盘中的阴影部分用一个“trominos”平铺，由归纳假设，余下的都可以用若干个“trominos”平铺。