黄金分割

1教材呈现

• 不同版本的初中教材中黄金分割基本上由比例中项定义线段的黄金分割与黄金分割点。
  

  1.1浙教版（安排在课时内容中）

  

  1.2北师大版（课时+阅读）

  

  1.3华师大版（阅读与思考）

  
  

思考：

• 1.黄金比的作法
  
• ⑴你能指出五角星中的黄金比吗？
• ⑵黄金比的作法。你还有其它的作法吗？

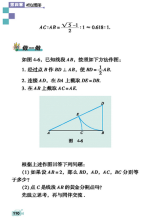
①利用勾股定理代数计算作出 \sqrt{5}

\Delta ABC , AB=1, AD= \dfrac{\sqrt{5}} {2}

AE=\dfrac{\sqrt{5}-1} {2}

• 点E是线段AB的黄金分割点；
  
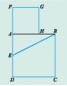
• 点H是线段AB的黄金分割点。

②利用顶角为36\degree的等腰三角形构造黄金比（实质上是因为\cos 36\degree = \dfrac{\sqrt{5}-1} {4}。

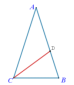
等腰三角形ABC中，\angle A =36\degree,\angle ACB的平分线 CD，点D是线段AB的黄金分割点.

• 拓展：
• ⑴黄金角。将线段类比到圆周，圆周有黄金分割与黄金分割点吗？你认为应该如何定义？
• 黄金角的构造如下：把长度为C的圆周分为两部分，各部分长度为 a 和 b ，也就是说 c=a+b，而它们的比例符合 c / a = a / b 长度为 b 的弧与圆心所成的角，也就是将圆周长依黄金比例分割成两段，大弧长所对应的圆心角约为222.49°，而小弧长所对应的圆心角约为137.51°称为黄金角。以弧度表示为：2π / φ²，这里 φ = (1+ 2.2360)÷2 约为1.618是黄金分割。最特别的一个是松果，它上面有左旋和右旋的阿基米德螺线，这些螺线的相邻交点的角度为黄金角。
• ⑵斐波那契数列：斐波那契数列1、2、3、5、8、13、21、34、55、89……的后一项与前一项的比趋向于黄金比。链接选择性改必修2阅读与思考《斐波那契数列》。
  

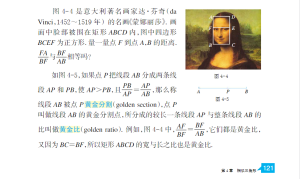
  2数学文化背景

• 黄金比例，这个神秘的词汇常常被赋予深奥而完美的意义，在艺术、建筑和自然界中无处不在。许多作者（包括《达·芬奇密码》的作者丹·布朗）将黄金分比例述为自然界美丽图案的基石，有时甚至被称为神圣比例。
• Chris Budd教授在一篇文章(plus.maths.org/content/myths-maths-golden-ratio译者：实验室的猫)中指出，它在历史长河中曾被赞誉为艺术和建筑的黄金法则，然而，实际证据却并不完全支持这种说法。帕特农神庙，被人们誉为“黄金比例”的典范，仔细测量却发现其并无完全符合。音乐大师莫扎特和贝多芬的作品，也并未严格遵循黄金比例。自然界中的黄金比例神迹也并未得到科学的证实。许多植物、生物的生长模式，并未完全契合黄金比例。牛顿认为太阳系的运转遵循黄金比例，但现今的模型计算已经否定了这一观点。但斐波那契数列确实出现在自然界中，因为它既与人口增长的方式有关，也与形状的拼接方式有关。许多自然现象确实与黄金分割、斐波那契数列有着密切的联系。例如我们可以在向日葵、菠萝、松果的螺旋中以及某些植物的叶子上观察到这个数列,是因为这样的排列，可以使种子得到最佳的堆集效果，彼此的生长空间相似，可以充分利用阳光和空气有利于后代繁衍。正视曾神话了黄金分割这些事实之后，黄金分割本身是多么惊人——它真的不需要那些虚假的主张来装扮它的独特魅力。
  

  3自然现象与黄金分割紧密关联的数学内核

• 植物的生长模式隐藏着了斐波那契数列，比如观察向日葵花冠，最先引起我们注意的是螺旋线，最外圈有55个花蕊沿顺时针方向排列，然后是34个反向排列，如果往中心方向看，有21个没顺时针方向，更接近中心有13个沿逆时针方向，相邻的数字出现在不同的区域，但他们总是有所重叠。植物在上述旋转生长中体现出一些共性。他们都从一个中心点开始生长，越来越多的花蕾从中心长出来，新长的种子会从相对有空隙的地方钻出,而将原先种子由内向外推挤，造就了美丽均质效果。
  
  
  
• 法国两位晶体学家奥古斯特和勃拉维兄弟发现了这个模式的秘密。最中心奥古斯特和勃拉维测量出每个新种子和前一个之间的角度为 137.51°,这个角度称为黄金角。
  
  
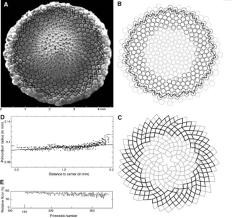
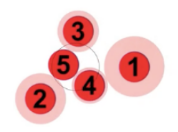
• 我们来做一个试验，根据内层的螺旋个数假定每个新种子与前一个种子之间的角度在3/8至5/13个圆周角之间，用计算机模拟原基细胞的生长过程。
  
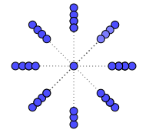
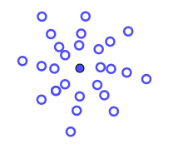
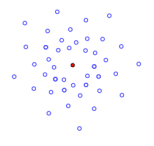
  135度（直线状） 135.5度（有间隙螺旋） 137.5度（均匀螺旋，顺时针8条、逆时针13条）
• 黄金分割具有惊人的特征,它是所有无理数中最无理的数，这意味着它不仅无法用分数精确表示,甚至很难用分数来近似表达它，植物花蕾按照这样的模式，所有种子都被压缩得非常紧密，每一个部分都有相同的结构，以最优最紧密的绕圈方式生长。
• 具体内容请看油管频道英国数学家伊恩·斯图尔特 Ian Stewart教授讲解的视频https://www.youtube.com/watch?v=mM1pKHTWkTg. 
  
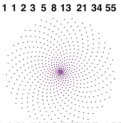
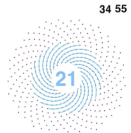
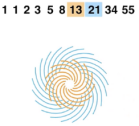
• 近距离观察，会看到顺时针与逆时针螺线，形成菱形的网格，第三种螺线穿过菱形网格的对角线。内层21条顺时针螺旋线，34条逆时针螺旋线，55条对角螺旋线（外层的顺时针螺旋线）。
  
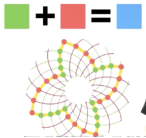
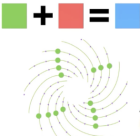
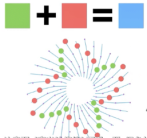
• 沿着顺时针螺线与逆时针螺线的交点作一个闭环。每个红点表示顺时针螺线，红点个数与顺时针螺线一样多；每个绿点表示逆时针螺线，绿点个数与逆时针螺线一样多。另一方面，总数是蓝色的对角线螺线。这样就证明了“红+绿=蓝”。
• 不同的植物可能有很多不同的序列，比如2，3，5，8，13……；4，6，10，16，26……；3，4，7，11，18……。但遵循相同的规则（每一项等于前两项之和）。
• 具体请看视频德国澳洲莫纳什大学的Burkard Polster教授《The fabulous Fibonacci flower formula》www.youtube.com/watch?v=_GkxCIW46to.
  

  4实践应用

• 我国著名数学家华罗庚倡导“0.618优选法”，在生产企业中推广应用取得了成效。华罗庚在他当时传阅甚广的著作《优选法平台及其补充》的第一章中，便详细介绍了用黄金比例分割取值区间来选择数据点的方法找单峰函数的极值，如图（图并非书中原图）： 
• 图片来源：https://en.wikipedia.org/wiki/Golden-section_search
  
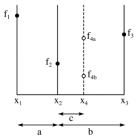
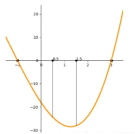
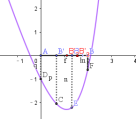
• 如图，对于单谷函数，我们假设f只有一个极小值（就是两边的值都比自身大的地方），而且 f 相对平滑。X 轴代表温度，纵向轴则代表时间。假设在这个例子中，中间点的相应值比边界的两个值都要小。我们先把具体值分别代入 x1 和 x3，分别算出 f1 和 f3，并取中间两个点 x2、x4（x2<x4），算出f2，f4。如果 f4> f2，因为是单谷函数，我们的下一步就应该在区间 [x1, x4]上找极小值点；同理，如果 f4< f2，我们的下一步就应该在区间 [x2, x3]上找极小值点。那么这和黄金比例有什么关系呢？
• 华罗庚推荐的这种优选法有两个核心理念：
• 第一、不论上一步的结果如何，下一步要测试的取值区间长度都应该相等；
• 第二、第二，每一步前后的取值区间长度比例也应该相等。
  根据这两个理念，我们得到以下两个式子：

x_4-x_1=a+b+c，\dfrac{x_3-x_2} {x_3-x_1} = \dfrac{b} {a+b} = \dfrac{b-c} {b} = \dfrac{x_3-x_4} {x_3-x_2}

把第一行式子代入到第二行，就可以得到，\dfrac{b} {a+b}。\dfrac{a}{b}正是黄金比约等于 0.618。使用黄金分割法的时候，x4恰是[x2, x3]黄金分割点,x2恰是[x1,x4]的黄金分割点，可以在下一次实验中复用，这样就大大减少了实验次数。

• 当然，现实中大部分函数都不会只有一个极值，而且也不会像我们这里假设的那样非常平滑。要想在这些复杂的情况中找到最优解的近似值，我们需要更复杂的计算和更多的步骤，但最终优选法的思路还是不变的：通过在现有区间的中间找数据点来不断缩小可能的取值区间，一直到足够精确（看不出上次和本次区别）或者次数已满，这时所采集的所有数据点中的最小值就是我们近似出的最优解。
  
• PS1：黄金分割法与二分法。黄金分割法适用于单峰函数找极值（收敛速度每次缩小0.618倍），二分法适用于单调函数找零点（收敛速度每次缩小0.5倍）。单峰函数找极值的时候，二分法是不能够一次实验就把可行区域一分为二，我们不能断言极值一定在左边或右边区域。实际上我们需要四个点，比如说四个点按顺序实验的结果是1, 2, 2.5, 1.5，那么极值一定在第二个点到第四个点之间，但不能确定是第三个点左侧还是右侧。因此，与单峰函数找极值比对的应该是三分法。
  
• PS2：黄金分割法与三分法。黄金分割法的本质是把区间分为三段，如果用三等分法，则每次取的点都不相同，通过黄金分割的比例，使得三分法的效果更优。单峰函数找极值适用黄金分割法，