1教材呈现

2数学文化背景
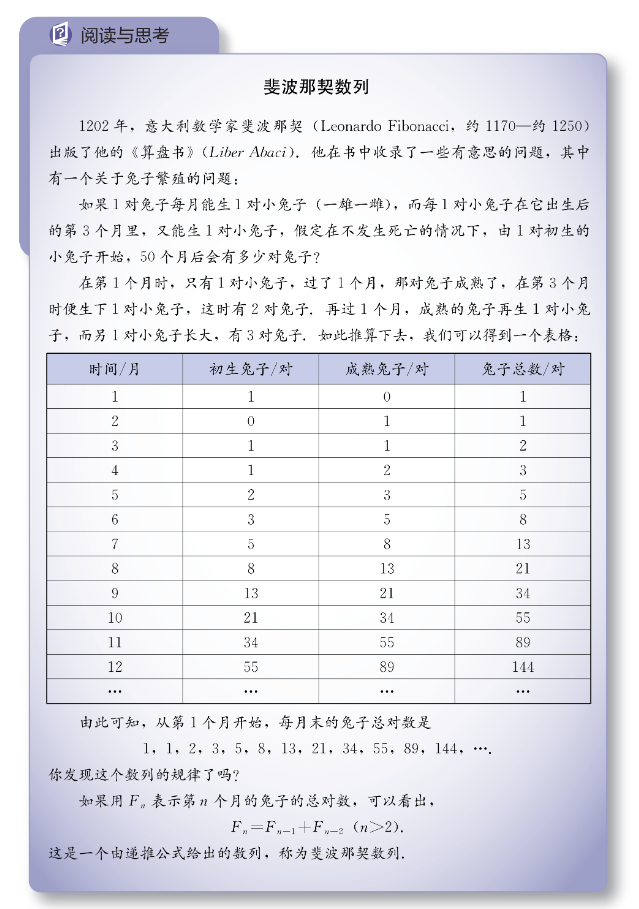
- 斐波那契数最早出现在1202年由比萨的列奥纳多(后来被戏称为“斐波那契”)所著的《算盘全书》中有一个有趣的兔子繁殖问题:如果每对兔子(一雄一雌)每月能生殖一对小兔子(假设也是一雄一雌,下同),每对兔子第一个月没有生殖能力,但从第二个月以后便能每月生殖一对小兔子。假定这些兔子都没有死亡现象,那么从第一对刚出生的兔子开始,12个月以后会有多少对兔子呢?解释说明为:第一个月:只有一对兔子;第二个月:仍然只有一对兔子;第三个月:这对兔子生殖了一对小兔子,共有1+1=2对兔子。第四个月:最初的一对兔子又生殖了一对兔子,共有2+1=3对兔子。则由第一个月到第十二个月兔子的对数分别是:1,1,2,3,5,8,13,21,34,55,89,144, ……,后人为了纪念提出兔子繁殖问题的斐波纳契,将这个兔子数列称为斐波那契数列,即把 1,1,2,3,5,8,13,21,34…这样的数列称为斐波那契数列。这个数列有一个很明显的特征,第0项为0,第1项为第一个1,数列从第2项开始每个数字都是前二项之和。有趣的是,随着数列数值的增加,前一项与后一项之比越来越接近黄金分割的数值 0.618……因此,斐波那契数列也被称为黄金分割数列。
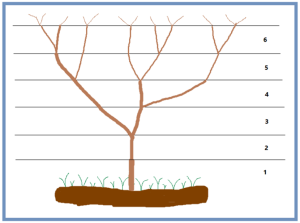
- 在自然界中,似乎完全没有秩序的植物彼此相隔的距离或叶子的生长,都被斐波那契数列支持着。例如一株树苗生长一年以后长出一条新枝;第二年新枝“休息”,老枝依旧萌发;此后,老枝与“休息”过一年的枝同时萌发,当年生的新枝则次年“休息”。这样,一株树木各个年份的枝桠数,便构成斐波那契数列。一朵花上的花瓣数量也通常是斐波那契数,如自然界中有1片花瓣的红掌花、牵牛花;2片花瓣的铁海棠、虎刺梅;3片花瓣的铁兰、三角梅(鸢尾花、百合花的花瓣看上去是6片,实际上是两套3片花瓣);5片花瓣的桃花、梅花;8片花瓣的飞燕草、波斯菊;13片花瓣的瓜叶菊、万寿菊;21片花瓣的紫菀等。



- 黄金比例,这个神秘的词汇常常被赋予深奥而完美的意义,在艺术、建筑和自然界中无处不在。有人指出,达芬奇的名画《蒙娜丽莎》存在大量的黄金比例。如图,从内到外依次连接通过小正方形的四分之一圆弧,得到一条被称为“斐波那契螺旋”的弧线。如果我们不断增加边长是斐波那契数的正方形,那么“斐波那契螺旋”也将不断向外延伸,而且它的形状将越来越接近“黄金比例螺旋”。(详见九年级“黄金分割”)
- 本节主要探究斐波那契数列最令人着迷的数字模式。
3斐波那契数列的数字规律
记斐波那契数列为\lbrace F_n \rbrace ,F_1=F_2=1,F_n=F_{n-1}+F_{n+1}。
3.1数列通项
- 思考一:从计数原理出发研究
为了说明方便引入数列\lbrace f_n \rbrace ,f_1=F_2,f_n=F_{n+1}(f_0=F_1),f_n=f_{n-1}+f_{n-2},斐波那契数列可以作为许多计数问题的解决方案,比如以下的模型都与斐波那契数列同构。
- 模型1:一步1个或2个台阶的爬n级楼梯;
- 模型2:如果一个节奏可以包含长度为1的短音节或长度为2的长音节,那么长度为n的节奏有多少个可能?即用11的正方形或12的多米诺骨牌平铺1*n长条

数学术语来表述:有多少种方法将n表示为数字1与2的和。
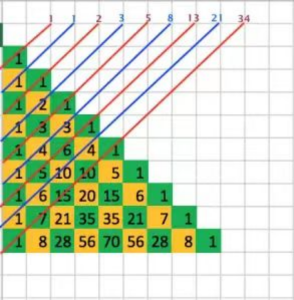
- 根据模型3,容易得到

C_6^0+C_5^1+C_4^2+C_3^3=f_6
即F_{n+1}=f_n=C_n^0+C_{n-1}^1+C_{n-2}^2+……+C_{n/2}^{n/2}为F_{n+1}=f_n=C_n^0+C_{n-1}^1+C_{n-2}^2+……+C_{(n-1)/2}^{(n-1)/2}
如C_8^0+C_7^1+C_6^2+C_5^3+C_4^4=F_{n+1}=f_9
- 思考二:从代数运算出发研究
(I)为什么前一项与后一项之比越来越接近黄金分割的数值 0.618……?
\dfrac{F_{n+1}}{F_n}=\dfrac{F_n+F_{n-1}}{F_n}=1+\dfrac{F_{n-1}}{F_n}
假设n\rarr\infty,\dfrac{F_{n+1}}{F_n}\rarr\phi,则有\phi=1+\dfrac{1}{\phi},即\phi=\dfrac{\sqrt{5}-1}{2}(\phi>0)。
(II)斐波那契数列的通项公式
F_{n+1}=F_n+F_{n-1},设F_{n+1}-sF_n=t(F_n-sF_n-1),则有,s+t=1,st=-1
s,t为方程x^2-x-1=0的两个根。
F_{n+1}-sF_n=t^{n-1}(F_2-sF_1)=t^n,同理F_{n+1}-tF_n=s^n
所以F_n=\dfrac{t^n-s^n}{t-s}=\dfrac{1}{\sqrt{5}}((\dfrac{1+\sqrt{5}}{2})^n-(\dfrac{1-\sqrt{5}}{2})^2)
3.2数列求和
1 = 1 = 2-1
1+1 = 2 = 3-1
1+1+2 = 4 = 5-1
1+1+2+3 = 7 = 8-1
1+1+2+3+5 = 12 = 13-1
1+1+2+3+5+8 = 20 = 21-1
1+1+2+3+5+8+13 = 33 = 34-1一般地,是否有F_1+F_2+F_3+…+F_n=F_{n+2}-1?
将每一项替换为两个斐波那契数之差裂项错位相消,得
F_1+F_2+F_3+…+F_n=
F_1+(F_3-F_1)+(F_4-F_2)+…+(F_{n-1}-F_{n-3})+(F_n-F_{n-2})+(F_{n+1}-F_{n-1})=F_{n+2}-1
推论1:F_2+F_4+…+F_{2n}=F_{2n+1}-1
推论2:F_1+F_3+…+F_{2n-1}=F_{2n}
3.3斐波那契数列的每一项平方得到的数列的数字规律

- 根据表格可以发现:
性质1:f_{2n}=f_n^2+f_{n-1}^2
推论:f_{m+n}=f_mf_n+f_{m-1}f_{n-1}
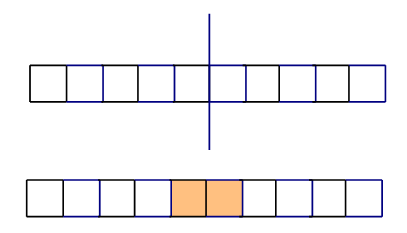
如图,利用模型2可以得到验证。将1n的长条分成两半,交接点有两种情况,断开或者连接在一起的12骨牌,所以有f_{2n}=f_n^2+f_{n-1}^2.
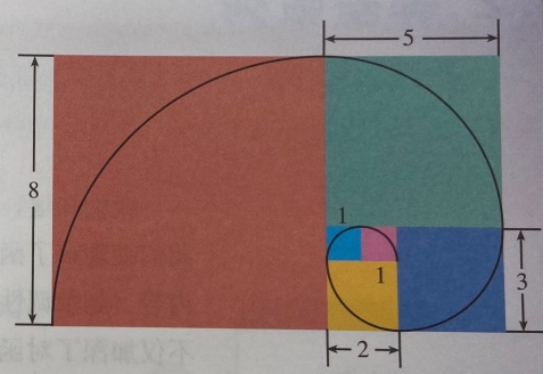
- 利用黄金矩形构成的螺旋图形,可以得到:
性质2:F_1^2+F_2^2+F_3^2+…+F_n^2=F_nF_{n+1}
推论:F_n^2-F_{n-1}F_{n+1}=\pm1
- 庞加莱:“所谓数学,本质上就是给不同事物起同一个名字。”当你发现两个事物具有相似的结构脉络或行为模式时,这种相似就建立了一种联系,你就发现了一种前所未有的实际意义。
文章评论